沪教版(新教材)数学必修 第三册第11章 简单几何体11.1 多面体与旋转体同步测试
一、选择题
由下列主体建筑物抽象得出的空间几何体中为旋转体的是( )
A.

B.

C.

D.


我要多选
作答:
答对了
答错了
一个几何体恰有6个顶点,则这个几何体可能是( )
A.
四棱柱
B.
四棱台
C.
五棱锥
D.
五棱台

我要多选
作答:
答对了
答错了
以下空间几何体是旋转体的是( )
A.
圆锥
B.
棱台
C.
正方体
D.
三棱锥

我要多选
作答:
答对了
答错了
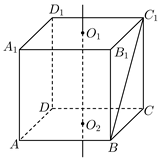
如图,已知正方体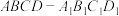 的上、下底面的中心分别为
的上、下底面的中心分别为 、
、 ,将正方体绕直线
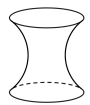
,将正方体绕直线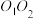 旋转一周,其中由线段
旋转一周,其中由线段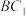 旋转所得图像是( )
旋转所得图像是( )
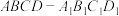 的上、下底面的中心分别为
的上、下底面的中心分别为 、
、 ,将正方体绕直线
,将正方体绕直线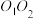 旋转一周,其中由线段
旋转一周,其中由线段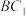 旋转所得图像是( )
旋转所得图像是( )
A.
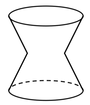
B.

C.
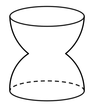
D.

我要多选
作答:
答对了
答错了
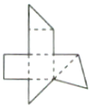
如图是一个简单多面体的表面展开图(沿图中虚线折叠即可还原),则这个多面体的顶点数为( )

A.
6
B.
7
C.
8
D.
9

我要多选
作答:
答对了
答错了
如图,正方体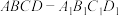 的棱长为1,线段
的棱长为1,线段 上有两个动点E、F,且
上有两个动点E、F,且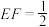 .结出结论:①AC⊥BE;②EF
.结出结论:①AC⊥BE;②EF 平面ABCD;③三棱锥A-BEF的体积为定值;④
平面ABCD;③三棱锥A-BEF的体积为定值;④ 的面积与△BEF的面积相等.其中正确的结论是( )
的面积与△BEF的面积相等.其中正确的结论是( )
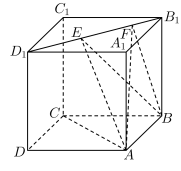
 的棱长为1,线段
的棱长为1,线段 上有两个动点E、F,且
上有两个动点E、F,且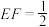 .结出结论:①AC⊥BE;②EF
.结出结论:①AC⊥BE;②EF 平面ABCD;③三棱锥A-BEF的体积为定值;④
平面ABCD;③三棱锥A-BEF的体积为定值;④ 的面积与△BEF的面积相等.其中正确的结论是( )
的面积与△BEF的面积相等.其中正确的结论是( )
A.
①②③;
B.
①②④
C.
②③④
D.
①③④

我要多选
作答:
答对了
答错了
将选项中所示的三角形绕直线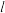 旋转一周,可以得到如图所示几何体的是哪一个三角形( ).
旋转一周,可以得到如图所示几何体的是哪一个三角形( ).
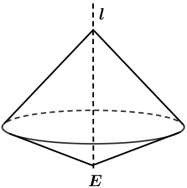
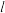 旋转一周,可以得到如图所示几何体的是哪一个三角形( ).
旋转一周,可以得到如图所示几何体的是哪一个三角形( ).
A.

B.
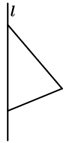
C.

D.
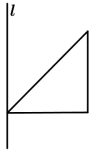

我要多选
作答:
答对了
答错了
一个棱锥被平行于底面的平面所截截面面积恰好是棱锥底面面积的一半,则截得的小棱锥与原棱锥的高之比是( )
A.

B.
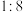
C.
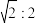
D.


我要多选
作答:
答对了
答错了
如图1所示,已知正方体面对角线长为a,沿阴影面将它切割成两块,拼成如图2所示的几何体,那么此几何体的表面积为( )


A.
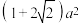
B.

C.
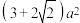
D.
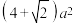

我要多选
作答:
答对了
答错了
如图所示的几何体,关于其结构特征,下列说法不正确的是


A.
该几何体是由两个同底的四棱锥组成的几何体
B.
该几何体有12条棱、6个顶点
C.
该几何体有8个面,并且各面均为三角形
D.
该几何体有9个面,其中一个面是四边形,其余均为三角形

我要多选
作答:
答对了
答错了
二、填空题
一个几何体有6个顶点,则这个几何体可能是______ 棱柱.

我要多选
作答:
答对了
答错了
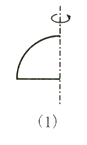
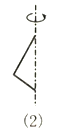
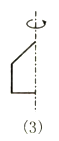
如图,第一排的图形绕虚线旋转一周能形成第二排中的某个几何体.请写出第一排、第二排中相应的图形的对应关系.

A. B.
B.  C.
C.  D.
D. 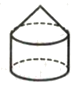
(1)_____ (2)_____ (3)_____ (4)_____




A.
 B.
B.  C.
C.  D.
D. 
(1)

我要多选
作答:
答对了
答错了
一个简单多面体的面都是三角形,顶点数 ,则它的面数为
,则它的面数为__ 个.
 ,则它的面数为
,则它的面数为
我要多选
作答:
答对了
答错了
已知过球面上三点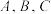 的截面到球心距离等于球半径的一半,且
的截面到球心距离等于球半径的一半,且 是边长为6的等边三角形,则球面面积为
是边长为6的等边三角形,则球面面积为__________ .
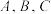 的截面到球心距离等于球半径的一半,且
的截面到球心距离等于球半径的一半,且 是边长为6的等边三角形,则球面面积为
是边长为6的等边三角形,则球面面积为
我要多选
作答:
答对了
答错了
一个圆台的母线长为20cm,母线与轴的夹角为30°,上底面半径为15cm,则下底面半径为___________ .

我要多选
作答:
答对了
答错了
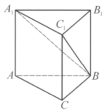
我国古代数学名著《九章算术》对立体几何也有深入的研究,从其中的一些数学用语可见,譬如“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.现有一如图所示的“堑堵”即三棱柱 ,其中
,其中 ,若
,若 ,当“阳马”即四棱锥
,当“阳马”即四棱锥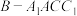 ,体积最大时,“堑堵”即三棱柱
,体积最大时,“堑堵”即三棱柱 的表面积为
的表面积为_______ .
 ,其中
,其中 ,若
,若 ,当“阳马”即四棱锥
,当“阳马”即四棱锥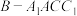 ,体积最大时,“堑堵”即三棱柱
,体积最大时,“堑堵”即三棱柱 的表面积为
的表面积为

我要多选
作答:
答对了
答错了
三、综合题
如图所示,图①是正方体木块,把它截去一块,可能得到的几何体有②③④⑤.




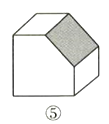
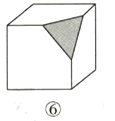
(1)我们知道,正方体木块有8个顶点,12条棱、6个面,请你将②③④⑤中木块的顶点数、面数填入下表:
(2)观察你填出的表格,归纳出上述各种木块的顶点数V、棱数E、面数F之间的关系.
(3)看图⑥中正方体的切法,请验证你所得的数量关系是否正确.






(1)我们知道,正方体木块有8个顶点,12条棱、6个面,请你将②③④⑤中木块的顶点数、面数填入下表:
| 图号 | 顶点数 | 棱数 | 面数 |
| ① | 8 | 12 | 6 |
| ② | |||
| ③ | |||
| ④ | |||
| ⑤ |
(2)观察你填出的表格,归纳出上述各种木块的顶点数V、棱数E、面数F之间的关系.
(3)看图⑥中正方体的切法,请验证你所得的数量关系是否正确.

我要多选
作答:
答对了
答错了
如图,以 的一边AB所在直线为轴,其他三边旋转一周形成的面围成一个几何体,画出这个几何体的图形,并说出其中的简单几何体及有关的结构特征.
的一边AB所在直线为轴,其他三边旋转一周形成的面围成一个几何体,画出这个几何体的图形,并说出其中的简单几何体及有关的结构特征.
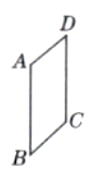
 的一边AB所在直线为轴,其他三边旋转一周形成的面围成一个几何体,画出这个几何体的图形,并说出其中的简单几何体及有关的结构特征.
的一边AB所在直线为轴,其他三边旋转一周形成的面围成一个几何体,画出这个几何体的图形,并说出其中的简单几何体及有关的结构特征.

我要多选
作答:
答对了
答错了
已知长方体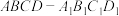 ,其中
,其中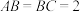 ,过
,过 三点的的平面截去长方体的一个角后,得到如图所示的几何体,这个几何体的体积为
三点的的平面截去长方体的一个角后,得到如图所示的几何体,这个几何体的体积为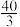 ,求几何体
,求几何体 的表面积.
的表面积.

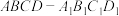 ,其中
,其中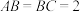 ,过
,过 三点的的平面截去长方体的一个角后,得到如图所示的几何体,这个几何体的体积为
三点的的平面截去长方体的一个角后,得到如图所示的几何体,这个几何体的体积为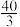 ,求几何体
,求几何体 的表面积.
的表面积.

我要多选
作答:
答对了
答错了
声明:本文档由用户提供并上传,仅供用户内部交流学习使用,若内容存在侵权,请点击举报删除。
贡献者:
 蒋亚
蒋亚