小明在组内经过合作交流,得到了如下的解决方法(如图1):
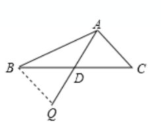
①延长AD到Q使得BQ=AD;
②再连接BQ,把AB,AC,2AD集中在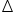 ABQ中
ABQ中
③利用三角形的三边关系可得4AQ
 14,则AD的取值范围是________
14,则AD的取值范围是________
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线。构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中。
阅读理解:课外兴趣小组活动时,老师提出了如下问题,在ABC中,AB=9,AC=5, BC边上的中线AD的取值范围
小明在组内经过合作交流,得到了如下的解决方法(如图1):

①延长AD到Q使得BQ=AD;
②再连接BQ,把AB,AC,2AD集中在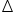 ABQ中
ABQ中
③利用三角形的三边关系可得4AQ
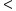 14,则AD的取值范围是________
14,则AD的取值范围是________
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线。构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中。
请写出图1中AC与BQ的位置关系并证明;
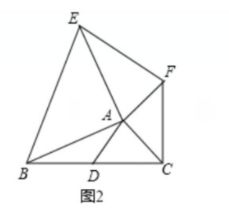
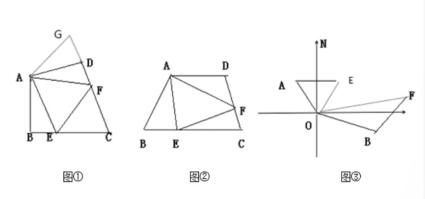
思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,![]() BAE=
BAE=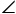 FAC=90
FAC=90![]() ,试探究线段AD与EF的数量和位置关系,并加以证明.
,试探究线段AD与EF的数量和位置关系,并加以证明.

如图,正方形ABCD中,E、F分别在边BC、CD上,且EAF=45
,连接EF,这种模型 属于“半角模型”中的一类,在解决“半角模型”问题时,旋转是一种常用的分析思路,例如 图中△ADF与△ABG可以看作绕点A旋转90
 的关系,这可以证明结论"EF=BE+DF”,请补充辅助线的作法,并写出证明过程
的关系,这可以证明结论"EF=BE+DF”,请补充辅助线的作法,并写出证明过程
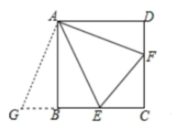
延长CB到点G,使BG=__,连接AG;
证明:EF=BE+DF

如图,已知AP//BC,PAB的平分线与
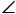 CBA的平分线相交于点E,CE的连线交AP于点D,求证:AD+BC=AB
CBA的平分线相交于点E,CE的连线交AP于点D,求证:AD+BC=AB

如图1:在四边形ABCD中,AB=AD,ZBAD=120°,ZB-ADC=90°,E、F分 别是BC,CD上的点,且EMF=60°,探究图中线段BE,EF,FD之间的数量关系, 小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连接AG,先证明△ABE
△ADG,再证明△AEF
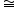 △AGF,即可得出BE,EF,FD之间的数量关系,他的结论应是__________.
△AGF,即可得出BE,EF,FD之间的数量关系,他的结论应是__________.
像上面这样有公共顶点,锐角等于较大角的一半,且组成这个较大角的两边相等的几何 模型称为半角模型,
拓展
如图2,若在四边形ABCD中,AB=AD,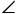 B+
B+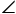 D=180°,E、F分别是BC,CD上的点,且
D=180°,E、F分别是BC,CD上的点,且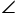 EAF=
EAF=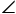 BAD,则BE,EF,FD之间的数量关系是________
BAD,则BE,EF,FD之间的数量关系是________
请证明你的结论:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在 指挥中心南偏东70°的B处,且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里小时 的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离是______海里(直接写出答案)

如图1,点P是MON角平分线上的一点,过点P作PA
OM于点A,PB
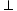 ON于点B.
ON于点B.
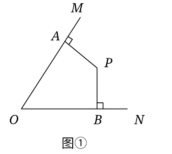
求证:PA=PB;
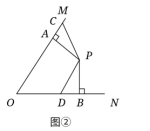
在(1)的条件下,如图2,点C是射线AM上一点,点D是线段OB上一点,且CPD+
 MON=180
MON=180,若OC=12,OD=6,求线段OB的长;
[探索升级]
如图3,仍然在(1)的条件下,若MON=60
,将PB绕点P以每秒2
 的速度顺时针旋转,12秒后,PA开始绕点P以每秒10
的速度顺时针旋转,12秒后,PA开始绕点P以每秒10 的速度顺时针旋转,PA旋转270
的速度顺时针旋转,PA旋转270 后停止,此时PB也随之停止旋转,旋转过程中,PA所在直线与OM所在直线的交点记为G,PB所在直线与ON所在直线的交点记为H,则PA旋转______秒时,PG=PH
后停止,此时PB也随之停止旋转,旋转过程中,PA所在直线与OM所在直线的交点记为G,PB所在直线与ON所在直线的交点记为H,则PA旋转______秒时,PG=PH
[灵活拓展]
如图4,四边形ABCD被对角线BD分为等腰RtABD和Rt
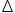 CBD,其中AB=AD,
CBD,其中AB=AD, BAD=
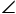 BCD=90
BCD=90,另一条对角线AC的长为4,则四边形ABCD的面积为_______
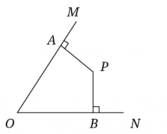

已知等边△ABC中,AC=AB=BC,BAC=
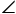 B=
B=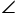 ACB=60
ACB=60,
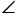 BAC与
BAC与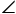 ACB的角平分线交于点O,且
ACB的角平分线交于点O,且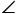 COA=120°OA=OC,点M,N分别在直线AC,AB上,且
COA=120°OA=OC,点M,N分别在直线AC,AB上,且 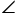 MON=60°,试猜想AM、 CN、MN三者之间的数量关系。
MON=60°,试猜想AM、 CN、MN三者之间的数量关系。
如图1,当CM=CN时,M、N分别在边AC、BC上时,我们可以在AM上截取AD=CN,连 接OD,先证明△OCN△_______ ,再证明△NOM
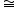 △_____ ,便可得出线段 AM、CN、MN三者之间的数量关系为_________;
△_____ ,便可得出线段 AM、CN、MN三者之间的数量关系为_________;
如图2,当CMCN时,M、N分别在边AC、BC上时,(1)中的结论是否仍然成立?若成立 请你加以证明,若不成立,请说明理由;
如图3,当点M在边AC上,点N在BC的延长线上时,请根据(1)中的证明过程
①在图3中作出辅助线;
②写出辅助线的作法;____________
③直接写出线段AM、CN、MN三者之间的数量关系:____________

 小玄
小玄