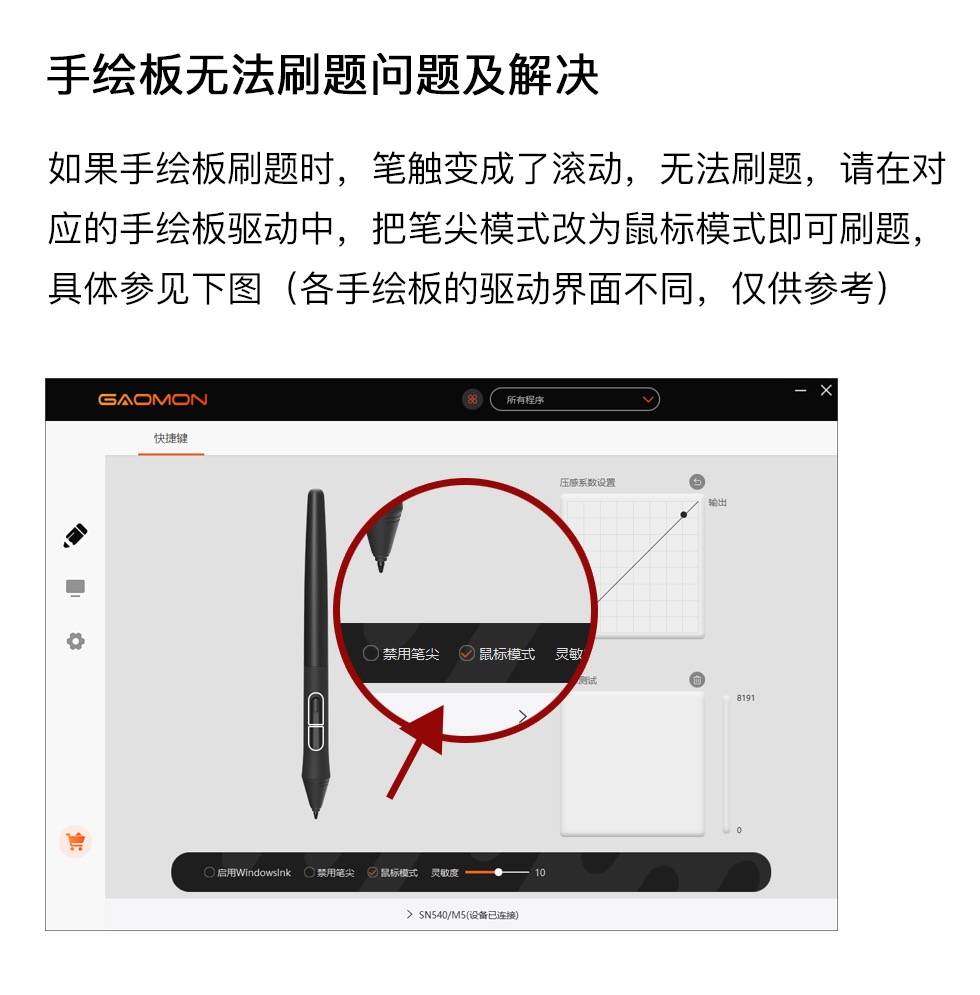
人教版八年级数学上册 14.3.2公式法（3） 同步测试
一、选择题
下列各式分解因式正确的是（ ）
A.
x2+6xy+9y2=（x+3y）2
B.
2x2﹣4xy+9y2=（2x﹣3y）2
C.
2x2﹣8y2=2（x+4y）（x﹣4y）
D.
x（x﹣y）+y（y﹣x）=（x﹣y）（x+y）
我要多选
作答：
答对了
答错了
a是有理数，则多项式﹣a2+a﹣ 
的值（ ）
的值（ ）A.
一定是正数
B.
一定是负数
C.
不可能是正数
D.
不可能是负数
我要多选
作答：
答对了
答错了
已知（2x-21）（3x-7）-（3x-7）（x-13）可分解因式为 （3x+a）（x+b） 其中a,b均为整数，则a+3b=（ ）
A.
30
B.
C.
31
D.
我要多选
作答：
答对了
答错了
把代数式2x2﹣18分解因式，结果正确的是（ ）
A.
2（x2﹣9）
B.
2（x﹣3）2
C.
2（x+3）（x﹣3）
D.
2（x+9）（x﹣9）
我要多选
作答：
答对了
答错了
对于非零的两个实数a，b，规定 
，那么将 
结果再进行分解因式，则为（ ）
，那么将 结果再进行分解因式，则为（ ） A.
a(a+2)(a-2)
B.
a(a+4)(a-4)
C.
(a+4)(a-4)
D.
a(a2+4)
我要多选
作答：
答对了
答错了
下列因式分解正确的是（ ）
A.
4m2-4m+1=4m（m-1）
B.
a3b2-a2b+a2=a2（ab2-b）
C.
x2-7x-10=（x-2）（x-5）
D.
10x2y-5xy2=5xy（2x-y）
我要多选
作答：
答对了
答错了
二、填空题
若a+b=2，ab=﹣3，则代数式a3b+2a2b2+ab3的值为________．
我要多选
作答：
答对了
答错了
分解因式：2a2﹣8b2=________．
我要多选
作答：
答对了
答错了
在实数范围内分解因式：a﹣4a3=________．
我要多选
作答：
答对了
答错了
因式分解：x2﹣x﹣12=________．
我要多选
作答：
答对了
答错了
若实数x满足x2﹣2x﹣1=0，则2x3﹣7x2+4x﹣2017=________．
我要多选
作答：
答对了
答错了
三、解答题
阅读材料：若m2﹣2mn+2n2﹣8n+16=0，求m、n的值．
解：∵m2﹣2mn+2n2﹣8n+16=0，
∴（m2﹣2mn+n2）+（n2﹣8n+16）=0
∴（m﹣n）2+（n﹣4）2=0，
∴（m﹣n）2=0，（n﹣4）2=0，
∴n=4，m=4．
根据你的观察，探究下面的问题：
1、
已知x2﹣2xy+2y2+6y+9=0，求xy的值；
2、
已知△ABC的三边长a、b、c都是正整数，且满足a2+b2﹣10a﹣12b+61=0，求△ABC的最大边c的值；
3、
已知a﹣b=8，ab+c2﹣16c+80=0，求a+b+c的值．
我要多选
作答：
答对了
答错了
分解因式
1、
x3﹣2x2+3x﹣2
2、
2x3+x2﹣5x﹣4
3、
x3﹣x2+2x﹣8．
我要多选
作答：
答对了
答错了
我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解．并规定：F（n）= 
．
． 例如12可以分解成1×12，2×6或3×4，因为12﹣1＞6﹣2＞4﹣3，所以3×4是12的最佳分解，所以F（12）= 
．
1、
如果一个正整数m是另外一个正整数n的平方，我们称正整数m是完全平方数．
求证：对任意一个完全平方数m，总有F（m）=1；
2、
如果一个两位正整数t，t=10x+y（1≤x≤y≤9，x，y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36，那么我们称这个数t为“吉祥数”，求所有“吉祥数”；
3、
在（2）所得“吉祥数”中，求F（t）的最大值．
我要多选
作答：
答对了
答错了
因式分解：
1、
20a3﹣30a2
2、
16﹣（2a+3b）2
3、
﹣16x2y2+12xy3z
4、
5x2y﹣25x2y2+40x3y
我要多选
作答：
答对了
答错了
分解因式：
1、
25（x+y）2﹣9（x﹣y）2
2、
m2﹣3m﹣28
3、
x2+x﹣20．
我要多选
作答：
答对了
答错了
声明：本文档由用户提供并上传，仅供用户内部交流学习使用，若内容存在侵权，请点击举报删除。
贡献者：
知夕斷卐
